MAKALAH MATEMATIKA KELAS 11: TURUNAN
Senin, Januari 29, 2018
Tambah Komentar
BAB I
PENDAHULUAN
A. Latar Belakang
Turunan merupakan salah satu dasar atau fondasi dalam analisis sehingga penguasaan terhadap berbagai konsep dan prinsip turunan fungsi dapat membantu dalam memecahkan suatu permasalahan dalam kehidupan sehari-hari. Suatu fungsi dapat dianalisis berdasarkan ide naik atau turun, keoptimalan, dan titik beloknya dengan menggunakan konsep turunan. Pada bagian berikut, kita akan mencoba mengamati berbagai permasalahan nyata dan mempelajari beberapa kasusdan contoh untuk menemukan konsep turunan.
Dalam kehidupan sehari-hari, kita sering menjumpai laju perubahan. Laju perubahan erat kaitannya dengan kecepatan. Pada pembahasan berikut, penulis terfokus pada subbab turunan fungsi aljabar.
B. Rumusan Masalah
1. Apa pengertian turunan ?
2. Bagaimanakah konsep turunan fungsi aljabar ?
C. Tujuan Penulisan
1. Mengetahui pengertian turunan
2. Mengetahui konsep rumus turunan aljabar
BAB II
PEMBAHASAN
A. Turunan Fungsi Aljabar
Dalam kehidupan sehari-hari kita sering menjumpai laju perubahan. Laju perubahan nilai fungsi meliputi laju perubahan rata-rata dan laju perubahan sesaat.
1. Laju Perubahan Rata-rata
a. Kecepatan Rata-rata
Andaikan sebuah benda P bergerak sepanjang garis koordinat dan posisinya pada saat t dinyatakan dengan s = f(t). Pada saat t=t1 benda berada di s1 = f(t1) dan pada saat t=t1+h, P berada di s2=f(t1+h).
Kecepatan rata-rata pada selang ini adalah 
b. Laju Perubahan Rata-Rata Nilai Fungsi
Definisi :

2. Laju Perubahan Sesaat
Misalkan sebuah benda P bergerak sehingga jarak benda s sebagai fungsi waktu t, ditentukan oleh persamaan s = f(t). Pada waktu t = t1 benda P berada di s1 = f(t1) dan pada saat t = (t1+h) benda P berada di s2 = f(t1+h) sehingga kecepatan rata-rata gerak benda P dalam selang 

dirumuskan sebagai berikut :

b. Laju Perubahan Nilai Fungsi
Definisi :
Misalkan fungsi y = f(x) terdefinisi di sekitar x = c. Laju perubahan sesaat nilai fungsi f di x = c dirumuskan sebagai berikut :

Contoh :
Perpindahan dari sebuah partikel yang bergerak sepanjang sebuah garis s diberikan oleh fungsi s(t) = 2t2 + 8t, t = 0; s dinyatakan dalam meter dan t dalam detik. Tentukan :
a. Kecepatan rata-rata pada 1 detik pertama
b. Kecepatan rata-rata pada 2 detik pertama
c. Kecepatan rata-rata dalam detik ke-2
d. Kecepatan rata-rata dalam detik ke-3
e. Kecepatan rata-rata dalam selang waktu 2 detik setelah satu detik pertama
f. Kecepatan rata-rata dalam selang waktu delta t detik setelah t detik pertama.
Jawab :

3. Definisi Turunan
Turunan dari suatu fungsi y = f(x) di titik x = c didefinisikan sebagai berikut.
Definisi :
Misalkan f adalah suatu fungsi dengan persamaan y = f(x) yang terdefinisi pada selang (interval) terbuka yang memuat c. Turunan pertama dari fungsi f di titik x = c atau laju perubahan sesaat dari y terhadap x di titik x = c, didefinisikan sebagai :
jika nilai limit ada.
Dengan memisalkan x = c+h pada definisi di atas, dapat dibuktikan bahwa definisi turunan pertama di titik x = c setara dengan :
B. Rumus Umum Turunan Fungsi
Definisi :
2. Rumus-Rumus Turunan Fungsi Aljabar
Pada subbab ini akan dibahas mengenai rumus-rumus untuk mencari turunan fungsi aljabar dengan menggunakan definisi turunan yang sudah dijelaskan pada bagian sebelumnya.
Contoh Soal

Jawab


LATIHAN


PEMBAHASAN


BAB III
PENUTUP
A. Kesimpulan
Pembahasan materi Turunan Fungsi Aljabar dapat diambil kesimpulan :
1. Aplikasi turunan fungsi aljabar dalam kehidupan sehari-hari dapat dijumpai pada laju perubahan
3. Rumus-rumus turunan fungsi aljabar
B. Saran
Penulis menyadari bahwa tulisan ini masih jauh dari sempurna, keddepannya penulis akan lebih fokus dan details dalam menjelaskan tentang penjelasan di atas dengan sumber-sumber yang lebih banyak yang tentunya dapat dipertanggung jawabkan.
DAFTAR PUSTAKA
(Online), (http://www.e-sbmptn.com/2014/12/soal-fungsi-turunan-matematika-dan.html, diakses 30 Maret 2016).
(Online), (http://www.matematikastudycenter.com/kelas-11-sma/100-turunan-fungsi-aljabar-11-sma#ixzz44pvtHTFB, diakses 30 Maret 2016).
Ponidi, dkk. 2006. Program Studi Ilmu Alam Matematika untuk SMA dan MA Kelas XI. Jakarta Timur: Widya Utama, hlm. 237 & 239.
Sinaga, Bornok. 2014. Matematika. Jakarta: Kemdikbud, hlm. 167.
Tampomas, Husein. 2006. Seribu Pena Matematika SMA Kelas XI. Jakarta: Erlangga, hlm. 352 –


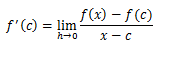




Belum ada Komentar untuk "MAKALAH MATEMATIKA KELAS 11: TURUNAN"
Posting Komentar
Tinggalkan komentar terbaik Anda...